[Machine Learning].Bayesian Classifier_이론

※ Bayesian Classifier (2-class-Classification)

Ex. 연어와 배스에 대해 구별하는 문제상황에 대해 생각해보자.

- 옵션1: 사람의 경험에 의해 어느 바다에서 어떤 물고기가 더 잘 잡히는지에 대한 연평균 데이터
- 옵션2: 자동적인 system [전처리-특징추출-classification]

class	X1 (Lightness)	X2 (Width)	Y (target)
Fish 1 Fish 2 . . . Fish n	. . .	. . .	Sea Bass Salmon Salmon

위의 class에 대해 우리는 분류를 해야하며 이때, Bayesian Classifier를 사용할 수 있는데,
다른 model들과 Bayesian이 가장 확연히 다른 점이 하나 있다. 아래 수식을 살펴보자.
먼저 Bayesian의 공식은 조건부확률로 이루어져 있다.

Bayes' Formula

여기서 가장 중요한 것은 Prior이다.

다른 머신러닝 모델들과 확연히 다른 Bayesian 만이 갖는 특징으로 사용자 주관이 개입될 수 있다는 점이다.

예를 들어 어떤 바다에서 물고기를 잡았을 때, 70%정도가 salmon이라 판별된다면,
이런 자연적인 분포비율을 model에 집어넣을 수 있다는 뜻이다.
예를 들어, 모델이 fish5에 대해 salmon일 확률을 0.3이라 예측했다면, 70%의 주관의 개입으로 모델의 분류효과를 달리할 수 있다는 점이다.

Likelihood만으로 측정한 결과값이 왼쪽이라면, 이 값에  prior를 추가해 오른쪽과 같은 값을 만들 수 있으며 좀 더 세밀한 분류도 가능해진다.

※ Generative vs Discriminative // Parametric vs Non-parametric

§ Generative vs Discriminative

▶ Generative
- modeling의 결과로부터 data를 만들 수 있다.
- Output: 확률 분포 (Probability distribution)

▶ Discriminative
- data를 모아 판별함수를 찾을뿐, 생성하지는 못하는 함수 (Just looking for a discriminant function)

§ Parametric vs Non-parametric

▶ Parametric
- 미리 지정된 모델의 파라미터를 최적화함 (optimize pre-defined parameters in a model)

▶ Non-parametric
- 모델에 파라미터자체가 없음 (no parameters in a model)

※ Parameter Estimation_ Discriminant Function for Decision Boundary

§ Decision Boundary

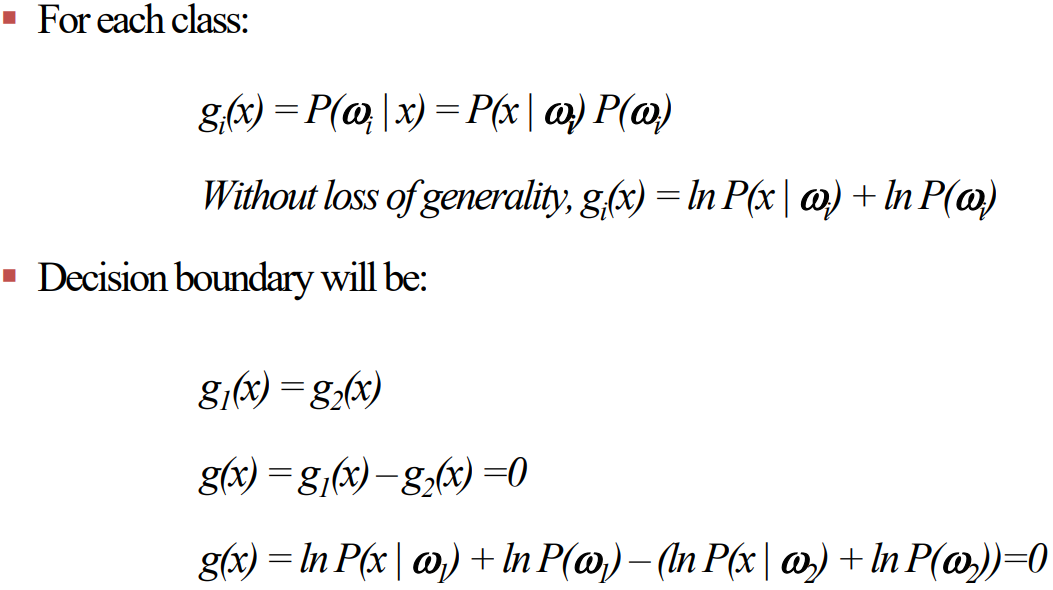
▶ 단항함수와 다항함수 Gaussian (Univariate and multivariate Gaussian)
- 단항함수 Gaussian (Univariate Gaussian)

뮤와 시그마 만 알면 값을 구할 수 있음

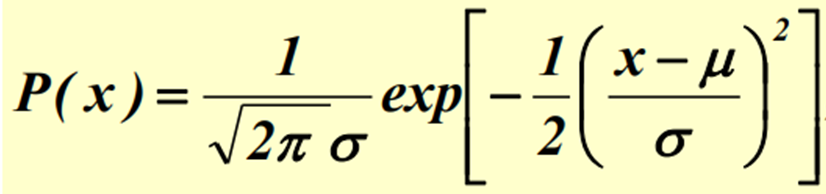
- 다항함수 Gaussian (Multivariate Gaussian)

d/2, 시그마, 뮤만 알면 값을 구할 수 있음

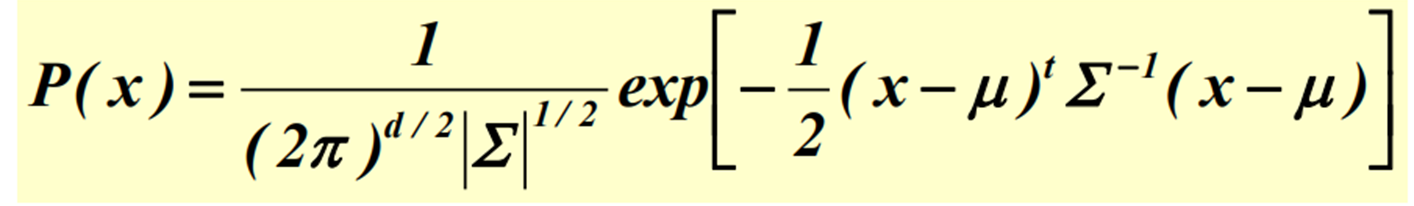
※ Maximum Likelihood Estimation

빨간색 점이 data를 뜻함

위 그래프에서 data 밀집이 평균과 가까워질수록 값이 커진다.
최댓값은 미분했을 때, 0일 때! (접선의 기울기 = 0)

§ 뮤(평균) 추정값

※ Naive Bayesian classifier

위와 같이 고차원 공간의 세타값 추정 방법

이 방법은 너무 복잡하고 시간소비가 심하다.

§ Naive Bayesian classifier => 매우 강한 추정방식 (모든 특징 변수들이 독립적이어서)

장점: 모든 변수가 다 독립이며 매우 string한 assumption이 가능하다.
따라서 각 클래스 별로 변수끼리 따로따로 계산해서 추정한다.

아래를 보면 Bayesian과 Naive간의 차이점을 볼 수 있다.

▶ 다중변수 추정을 나이브하게 만들어 단변수 추정으로 만들 수 있다.
(Multivariate distribution estimation => Univariate distribution estimation)