※ Recursion (순환 / 재귀)
흔히들 재귀라 부르는 recursion은 함수가 자기자신을 호출하여 문제를 해결하는 프로그래밍 기법이다.
보통 우리는 이렇게 반복을 요하는 문제에서는 반복문(for, while)을 사용하는 경우가 많다. 또한, 이런 반복문의 효율성은 무시하지 못할 것이다. 일반적으로 재귀보다는 반복문이 더욱 효율적이고 값 도출시간도 빠르다.
§ 최대공약수
auto gcd(int A, int B){
if (B == 0)
return A;
else
return gcd(B, A%B);
}https://chan4im.tistory.com/58
[Baekjoon/백준] 13241번: [Recursion] (C/C++) ★★☆
※ 이번 문제에서 알게된 점 § 재귀함수로 구현하는 gcd, lcm 함수 // 최대공약수 auto gcd(long long A, long long B){ if (B == 0) return A; else return gcd(B, A%B); } // 최소공배수 auto lcm (long long A, long long B){ return A*B
chan4im.tistory.com
https://www.acmicpc.net/problem/13241
13241번: 최소공배수
정수 B에 0보다 큰 정수인 N을 곱해 정수 A를 만들 수 있다면, A는 B의 배수이다. 예: 10은 5의 배수이다 (5*2 = 10) 10은 10의 배수이다(10*1 = 10) 6은 1의 배수이다(1*6 = 6) 20은 1, 2, 4,5,10,20의 배수이다. 다
www.acmicpc.net
※ 재귀를 사용하는 이유
이렇게 반복문보다 효율이 떨어지는 재귀를 도대체 우리는 사용하는 이유와 배워야 하는 이유가 무엇일까?
바로 재귀만이 갖는 자기자신의 호출로 특정 문제나 알고리즘에서 매우 강력(powerful)한 경우가 있다.
재귀로 짜면 간단하게 2~3줄로 나올 코드가 반복문으로 몇십줄이 넘어갈 수 도 있으니 말이다.
대표적인 예를 들어보자면 다음과 같다.
- 거듭제곱, 팩토리얼의 계산
백준 10872번: https://www.acmicpc.net/problem/10872
10872번: 팩토리얼
0보다 크거나 같은 정수 N이 주어진다. 이때, N!을 출력하는 프로그램을 작성하시오.
www.acmicpc.net
- 피보나치 수열의 계산
백준 2747번: https://www.acmicpc.net/problem/2747
2747번: 피보나치 수
피보나치 수는 0과 1로 시작한다. 0번째 피보나치 수는 0이고, 1번째 피보나치 수는 1이다. 그 다음 2번째 부터는 바로 앞 두 피보나치 수의 합이 된다. 이를 식으로 써보면 Fn = Fn-1 + Fn-2 (n ≥ 2)가
www.acmicpc.net
- 하노이탑 문제
백준 1914번: https://www.acmicpc.net/problem/1914
1914번: 하노이 탑
세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로
www.acmicpc.net
#include <iostream>
using namespace std;
int fac(int num){
if (num > 1)
return num * fac(num-1); // num: 해결된 부분 // fac(num-1): 남은부분
else
return 1;
}
int main() {
int num;
cin >> num;
cout << fac(num);
}이때, 재귀를 멈추는 부분
if (num > 1)
return num * fac(num-1);
else
return 1;위와 같은 재귀를 멈추는 부분이 없다면 시스템 stack을 모두 사용한 이후 Err가 발생하며 멈출 것이다. (stackoverflow)
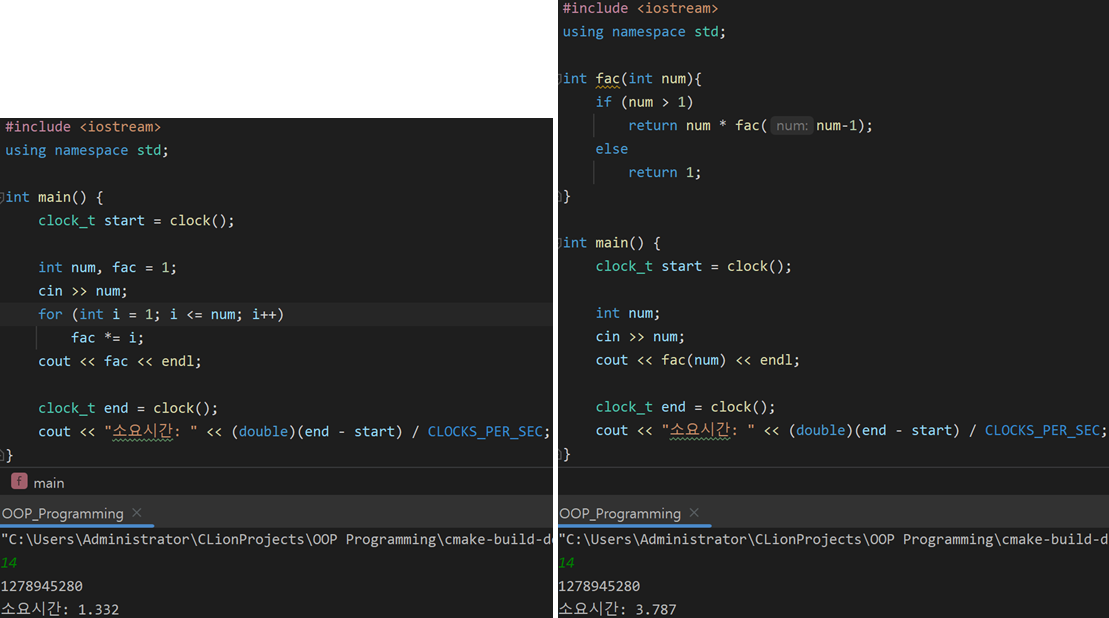
이렇게 반복에 비해 알고리즘을 훨씬 명확하고 간결하게 나타낼 수 있다는 장점이 있으나 아래와 같이 수행속도면에서는 현저히 떨어지는 것을 볼 수 있다.
※ Recursion의 시간복잡도
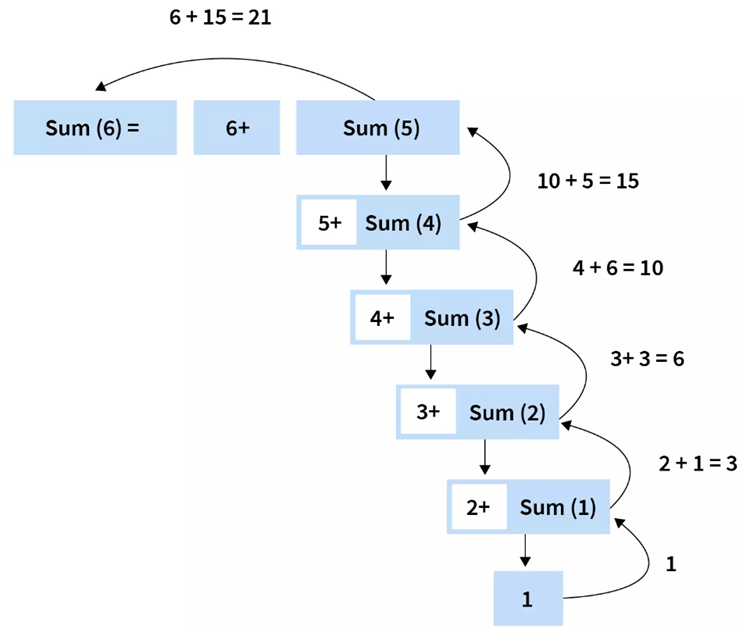
재귀는 작은 동일한 문제들로 분해하여 해결하는 방법인 분할정복 알고리즘의 일종이다.
5! -> 4! -> 3! -> 2! -> 1! 으로 작은 문제 즉, 본래의 problem을 subproblem으로 나누어 최소 size부터 해결하는 방식이다.
최소 subproblem부터 다시 본래의 problem size로 돌아가면서 정복하는, 이런 방식을 분할정복 알고리즘이라 부른다.
그렇다면 이런 재귀함수의 시간복잡도 즉, 성능은 어떻게 될까?
이를 위한 예시는 피보나치 수열문제로 한다.
int fib(int num){
if (num <= 1)
return num;
else
return fib(num-1) + fib(num-2);
}위의 문제에서 피보나치식의 n번째 계산을 위한 연산횟수를 T(n)이라 하자.
T(0) = 1, T(1) = 1이므로
T(n) = T(n-1) + T(n-2) + 1 > 2 x T(n-2) > 2x2 x T(n-4) > . . . 2 ^ (n/2) x T(0)이므로

int fib(int num){
int arr[100] = { 0, 1, };
if (num < 2 || arr[num] != 0)
return arr[num];
else{
arr[num] = fib(num-1) + fib(num-2);
return arr[num];
}
}그렇다면 다음 예제는 어떨까?
이 기법은 이미 구한 값을 메모리에 저장해두고 다시 사용하는 메모이제이션 (memoization)을 채택한 방법이다.
위 방법의 시간복잡도를 구해보면
T(0) = 1, T(1) = 1이고
T(2) = T(1) + T(0) + 1 = 3
T(3) = T(2) + T(1) + 1 = 5
T(4) = T(3) + T(2) + 1에서 T(2)는 저장한 피보나치 수를 가져오기만 하면 되기 때문에 T(2) = 1이다.
T(3) + T(2) + 1 = 7이고, 같은 이유로 T(5) = T(4) + T(3) + 1에서 T(3) = 1이므로 T(5) = 9이다.
따라서 T(n) = 2n - 1이라고 할 수 이므로

※ 다중 순환 (multiple recursion)
재귀함수는 아래와 같이 3종류로 나눌 수 있다.
- 선형 순환 (linear recursion)
ex) 팩토리얼계산, 거듭제곱 계산
- 이진 순환 (binary recursion)
ex) 피보나치수열, 하노이탑 문제
- 다중 순환 (multiple recursion)
'C | C++ > Data Structure & STL' 카테고리의 다른 글
| this.code(6).DS_ Tree, Binary Tree (0) | 2023.01.02 |
|---|---|
| this.code(5).DS_ List (4) | 2022.12.23 |
| ★this.code(3).DS_ Queue & (STL): queue, deque (0) | 2022.10.30 |
| this.code(2).DS_ Stack & Stack Container(STL) (0) | 2022.10.29 |
| this.code(1).DS_ Array & Vector (STL) (★★★★★★) (0) | 2022.10.28 |