※ 선형 자료구조
앞서 우리가 배운 것들은 모두 선형 자료구조에 속하는데 대표적으로 다음과 같다.
- stack, queue, deque, list . . .
여기서, list와 관련해 알아보고자 한다.
cf-1). stack, queue, deque 자료구조와 list의 차이는 무엇일까?
=> 항목에 대한 접근방법이다.
- 스택,큐: 전단(front), 후단(rear)에 접근방식이 제한되어 새로운 객체 삽입 삭제 시 중간에 하는 것을 허용X
- 리스트: 위와 달리 임의의 위치에 있는 항목에 대한 연산이 되기에 선형 자료구조들 중 가장 활용이 자유롭다.
cf-2) 연결리스트와 리스트의 용어의 차이는 무엇일까?
- 리스트: 특정 자료구조를 말하는 것으로 대응되는 키워드는 스택, 큐 등이다
- 연결리스트: 그런 자료구조를 구현하는 프로그래밍 기법으로 대응되는 키워드는 배열과 같은 뉘앙스이다.
※ 선형 리스트 (Linear List)
리스트(list) 또는 선형 리스트(linear list)라 불리는 자료구조는 항목들이 순서나 위치를 갖는 것이다.
- array, stack, queue, deque, list . . .
이때, 리스트와 집합이 다르다는 것을 알아야 한다.
- list(리스트): 각 항목간의 리스트에 들어있는 항목들 사이 순서가 존재한다.
- set(집합): 각 항목간의 순서의 개념이 없다.
또한 리스트는 자유로운 데이터 접근 방식으로 다양한 연산이 가능하다.
insert(pos, item) // 리스트의 pos위치의 새 요소, item 삽입
delete(pos) // 리스트의 pos위치의 요소 삭제
getEntry(pos) // 리스트의 pos위치의 요소 반환
find(item) // 리스트에 item이 있는지 검사
replace(pos, item) // 리스트의 pos위치에 있는 요소를 item으로 바꿈
isEmpty() // 리스트가 비어있는지 검사
isFull() // 리스트가 가득 차있는지 검사
size() // 리스트 안의 요소개수를 반환
display() // 리스트 안의 모든 요소 출력
리스트를 구현하는 방식은 배열을 사용하는 방법과 연결리스트 방식으로 나눌 수 있는데 보통 연결리스트를 사용한다.
배열 구현의 장점: ADT를 가장 간단하게 구현할 수 있다.
배열 구현의 단점: 요소의 개수에 제한이 생기며 메모리 낭비 및 비효율성과 삽입 삭제시 많은 요소의 이동 등이 있다.
연결리스트의 장점: 필요 시에만 노드를 동적으로 생성해 연결하며 연속된 메모리 공간을 할당할 필요도 없다.
연결리스트의 단점: 배열에 비해 구현이 복잡하다.(= 프로그래밍이 어려워지고 오류발생가능성이 커짐)
또한 할당과 해제가 빈번하게 일어나 프로그램이 느려질 수 있다는 단점도 존재한다.
따라서 보통 포인터를 사용한 연결리스트(Linked List)로 구현하는데, 이 방법도 다음 3가지 방법으로 나눌 수 있다.
단일 연결리스트 / 원형 연결리스트 / 이중 연결리스트
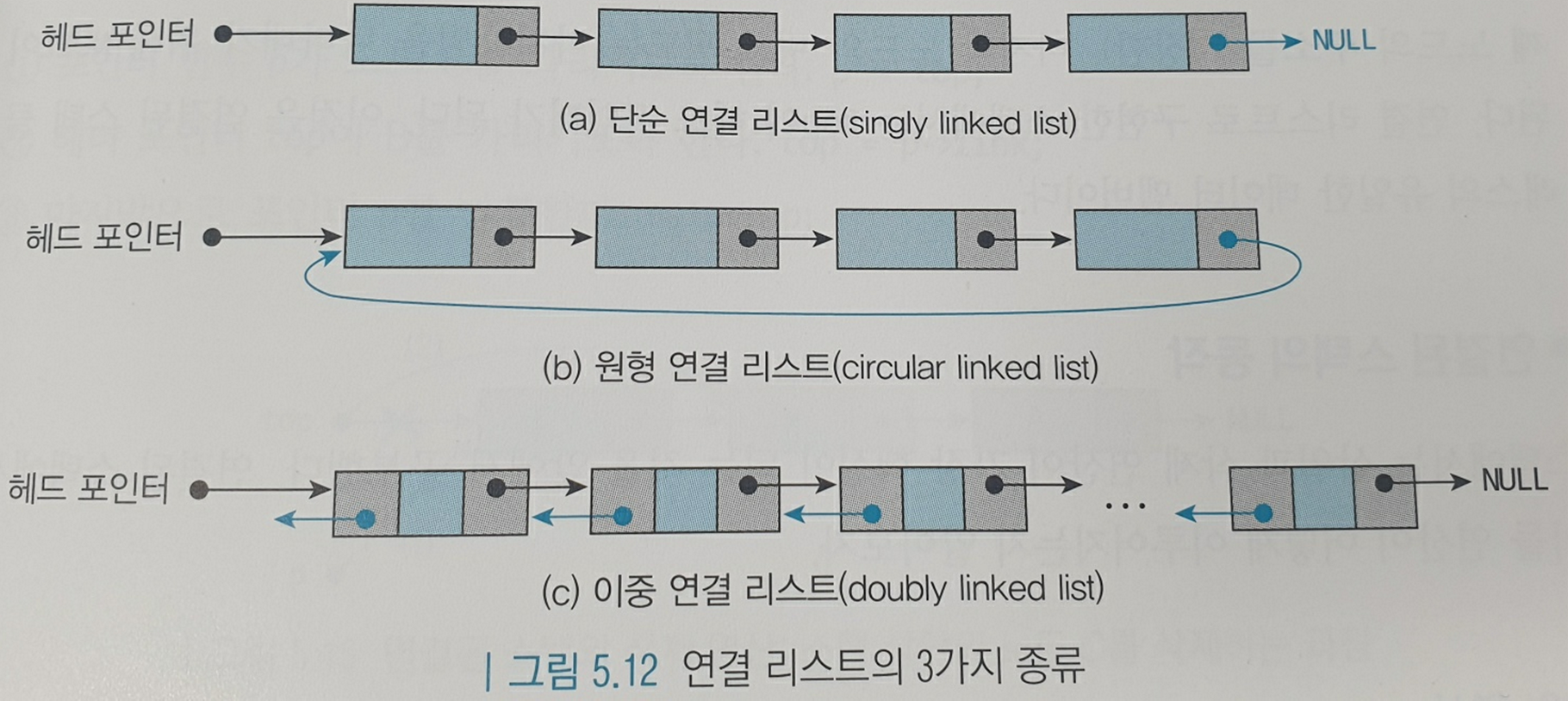
※ 연결 리스트 구현
§ 단일 연결리스트 (Single Linked List)
- 삽입과정 (insertion)

- 삭제과정 (deletion)

[구현]

[Node class_header file]
#include <iostream>
class Node{
private:
int data; // node의 data 필드
Node *link; // 다음 node를 가리키는 포인터변수
public:
Node(int val) : data(val), link(nullptr) {}
Node *getLink() { return link; }
void setLink(Node *next) { link = next; }
void display(){ printf(" <%2d>", data); }
bool hasData(int val) { return data == val;}
void insertNext(Node *node) {
if (node != nullptr){
node->link = link; // 새로운 node의 link를 선행하는 node와 연결
link = node; // 후속 node의 link와 새 node를 연결
}
}
Node *removeNext(){
Node *removed = link;
if (removed != nullptr)
link = removed->link; // 현재 node의 link를 다음다음 node의 data와 연결
return removed; // 삭제된 node주소를 반환해야 함. 그렇지 않으면 삭제된 node메모리가 해제되지 않고 위치를 잃어버림
}
};[Linked List class_header file]
[main_cpp file]
#include "LinkedList.h"
int main() {
LinkedList list;
list.insert(0, new Node(10)); // 리스트 맨 앞 10 삽입
list.insert(0, new Node(20)); // 리스트 맨 앞 20 삽입
list.insert(1, new Node(30)); // 리스트 1위치에 30 삽입
list.insert(list.size(), new Node(40)); // 리스트 마지막에 40 삽입
list.insert(2, new Node(50));
list.display();
list.remove(2); // 리스트 2위치 삭제
list.remove(0); // 리스트 맨 앞 삭제
list.replace(1, new Node(365)); // 리스트 1위치 값 365로 변경
list.display();
list.clear(); // 리스트 모든 항목 삭제
list.display();
}
§ 이중 연결리스트 (Doubly Linked List)
이중 연결리스트에서 임의의 node를 가리키는 포인터를 p라하면 아래와 같은 관계가 항.상! 성립한다.
p == p->next->prev == p->prev->next
- 삽입과정 (insertion)

- 삭제과정 (deletion)

[구현]
[Node2 class_header file]
#include <iostream>
class Node2{
private:
int data; // node의 data 필드
Node2 *prev; // 선행 node를 가리키는 포인터
Node2 *next; // 후속 node를 가리키는 포인터
public:
Node2(int val) : data(val), prev(nullptr), next(nullptr) {}
Node2 *getPrev() { return prev; }
Node2 *getNext() { return next; }
void setPrev(Node2 *p) { prev = p; }
void setNext(Node2 *n) { next = n; }
void display() { printf(" <%2d>", data); }
bool hasData(int val) { return data == val; }
void insertNext (Node2 *node) {
if (node != nullptr){
// 삽입 node의 prev가 삽입node의 prev node의 data를 가리킴
node->prev = this;
// 삽입 node의 next가 삽입node의 next node의 data를 가리킴
node->next = next;
// 삽입 node의 next node의 prev link가 삽입node의 data를 가리킴
if (next != nullptr)
next->prev = node;
// 삽입 node의 prev node의 next link가 삽입node의 data를 가리킴
next = node;
}
}
Node2 *remove() {
if (prev != nullptr)
return prev->next = next; // 현재 node기준 선행 node의 link가 후속 node의 data를 가리킴
if (next != nullptr)
return next->prev = prev; // 현재 node기준 후속 node의 link가 선행 node의 data를 가리킴
}
};
[DBLinkedList class_header file]
[main_cpp file]
#include "DBLinkedList.h"
int main() {
DBLinkedList list;
list.insert(0, new Node(10)); // 리스트 맨 앞 10 삽입
list.insert(0, new Node(20)); // 리스트 맨 앞 20 삽입
list.insert(1, new Node(30)); // 리스트 1위치에 30 삽입
list.insert(list.size(), new Node(40)); // 리스트 마지막에 40 삽입
list.insert(2, new Node(50));
list.display();
list.remove(2); // 리스트 2위치 삭제
list.remove(0); // 리스트 맨 앞 삭제
list.replace(1, new Node(365)); // 리스트 1위치 값 365로 변경
list.display();
list.clear(); // 리스트 모든 항목 삭제
list.display();
}
※ List Container (STL)
1. 관련 함수
§ iterator
begin(): beginning iterator 반환
end(): end iterator 반환
*iterator: iterator가 가리키는 원소에 접근
front(): 첫번째 원소 반환
back(): 마지막 원소 반환
§ 삽입 (insertion)
push_front(element): 리스트 맨 앞에 원소 추가
push_back(element): 리스트 맨 뒤에 원소 추가
insert(iterator, element): iterator가 가리키는 부분의 앞에 원소 추가
§ 삭제 (deletion)
pop_front(): 리스트 맨 앞의 원소 삭제
pop_back(): 리스트 맨 뒤의 원소 삭제
erase(iterator): iterator가 가리키는 부분의 원소 삭제
§ etc.
empty(): 리스트가 비어있는지 여부
size(): 리스트 사이즈 반환
2. 예시
#include <iostream>
#include <list>
using namespace std;
int main()
{
// 리스트 생성
list<int> a;
// 원소 추가
a.push_back(22);
a.push_back(33);
a.push_front(11);
a.push_back(44);
a.push_back(55);
// 반복자 생성
list<int>::iterator iter = a.begin();
// 리스트 출력
for(iter=a.begin(); iter!=a.end(); iter++)
{
cout << *iter << endl; // 원본 리스트: 11 22 33 44 55
}
cout << "" << endl;
cout << "" << endl;
// 원소 삭제
a.pop_front();
a.pop_back();
for(iter=a.begin(); iter!=a.end(); iter++)
{
cout << *iter << endl; // 원소 삭제후 리스트: 22 33 44
}
cout << "" << endl;
// 리스트 사이즈 출력
cout << a.size() << endl; // 3 출력( 22, 33, 44 이므로)
// 리스트가 비어있는가
cout << a.empty() << endl; // 비어있지 않으므로 0 반환
// 리스트 첫번째 원소 출력
cout << a.front() << endl; // 22
// 리스트 마지막 원소 출력
cout << a.back() << endl; // 44
cout << "" << endl;
// 반복자 2번째 위치로 이동
iter++; // 반복자가 두번째 원소(33)를 가리킴
iter++; // 반복자가 세번째 원소(44)를 가리킴
a.insert(iter, 55555);
for(iter=a.begin(); iter!=a.end(); iter++)
{
cout << *iter << endl; //세번째 원소(44) 전에 추가하는 것(22,55555,33,44)
}
}
'C | C++ > Data Structure & STL' 카테고리의 다른 글
| this.code(7).DS_ BST (Binary Search Tree). & AVL tree (0) | 2023.01.02 |
|---|---|
| this.code(6).DS_ Tree, Binary Tree (0) | 2023.01.02 |
| this.code(4).DS_ Recursion (재귀)_최대공약수 (0) | 2022.10.30 |
| ★this.code(3).DS_ Queue & (STL): queue, deque (0) | 2022.10.30 |
| this.code(2).DS_ Stack & Stack Container(STL) (0) | 2022.10.29 |