※ 정렬 (Sorting)
정렬은 오름차순, 내림차순과 같은 방식으로 특정 필드값인 key를 기준으로 value간의 정렬을 진행해 주며 다음 2가지로 나뉜다.
단순, 비효율적 방법: 삽입, 선택, 버블 정렬 ==> 대개 자료의 개수가 적을 때 사용
복잡, 효율적인 방법: 힙, 합병, 퀵 정렬 ==> 반드시 자료의 개수가 많다면 효율적 알고리즘을 사용해야 함.

🧐 간단하지만, 비효율적인 정렬 방법
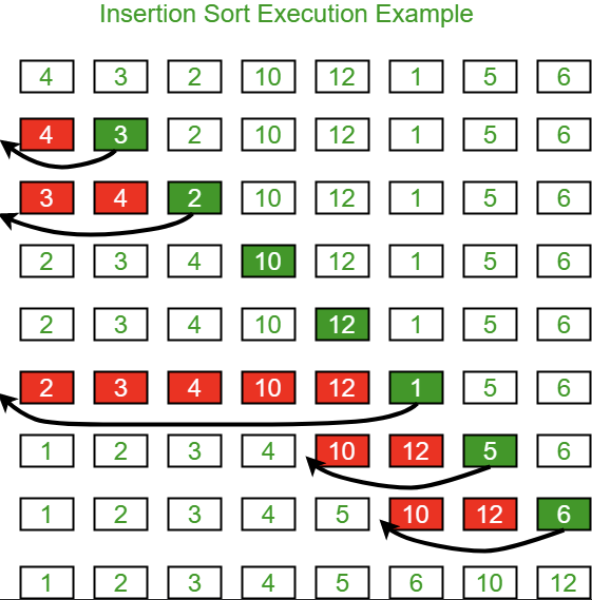
👉 삽입 정렬 (insertion Sort)
삽입정렬은 마치 카드놀이 새 카드를 받는 것 처럼 정렬한 카드들 사이의 올바른 자리에 넣는 것이다.
삽입정렬 방식은 다음과 같이 진행된다.
🤨 insertion sort Algorithm
insertionSort(A, n)
for i <- 1 to n-1 do
key <- A[i];
j <- i-1;
while j ≥ 0 and A[j] > key do
A[j+1] <- A[j];
j <- j-1;
A[j+1] <- key
void insertionSort (int A[], int n) {
for (int i = 0; i < n; i++) {
int key = A[i];
int j;
for (j = i-1; j >= 0 && A[j] > key; j--)
A[j+1] = A[j];
A[j+1] = key;
}
}
👉 선택 정렬 (Selection Sort)
가장 이해하기 쉬운 정렬방법으로 오른쪽 리스트가 공백상태가 될 때까지
오른쪽 리스트에서 왼쪽리스트로 가장 작은 숫자를 선택해 이동시킨다.
이렇게 입력배열 이외에 다른 추가 메모리를 요구하지 않는 정렬방법을 제자리 정렬이라 한다.

🤨 selection sort Algorithm
selectionSort (A, n)
for i <- 0 to n-2 do
least <- A[i], A[i+1], . . . , A[n-1] 중 가장 작은 값의 idx;
A[i]와 A[least]의 교환;
i++;
void selectionSort (int A[], int n) {
for (int i = 0; i < n-1; i++) {
int least = i;
for (int j = i+1; j < n; j++)
if (A[j] < A[least])
least = j;
swap(A[i], A[least]);
}
}
👉 버블 정렬 (Bubble Sort)
마치 거품이 일어나듯 인접한 2개의 인덱스 값들을 서로 비교하여 큰 값을 오른쪽에 두도록 서로 swapping 하는 것으로 과정은 아래와 같다.

🤨 bubble sort Algorithm
BubbleSort(A, n)
for i <- n-1 to 1 do
for j <- 0 to i-1 do
j와 j+1번째의 요소가 크기순이 아니면 swap
j++;
i--;
void bubbleSort (int A[], int n) {
for (int i = n-1; i >= 0; i--) {
for (int j = 0; j < i; j++)
if (A[j] > A[j+1])
swap(A[j], A[j+1]);
}
}
'C | C++ > Data Structure & STL' 카테고리의 다른 글
| this.code(9).DS_ sort I. [heap, merge, quick]sort (0) | 2023.01.03 |
|---|---|
| this.code(8).DS_ Priority Queue. &. Heap (0) | 2023.01.03 |
| this.code(7).DS_ BST (Binary Search Tree). & AVL tree (0) | 2023.01.02 |
| this.code(6).DS_ Tree, Binary Tree (0) | 2023.01.02 |
| this.code(5).DS_ List (4) | 2022.12.23 |