1.2 행렬 곱셈 AB
내적(행과 열의 곱셈)은 AB = C의 각 성분 계산을 위해 필요
ex) A의 2행 , B의 3열간의 곱셈의 합은 C의 c₂₃의 값이다.※ 선형대수학 제 1정리
· row rank = column rank
· r개의 일차독립 열(column) ↔ r개의 일차독립 행(row)
1.2.1 AB = (rank 1인 행렬의 합)
AB = A열과 B행의 곱셈이라 하자.cf) AB = (m×n)(n×p) , 총 mnp의 곱셈 연산수
cf-1) 행×열: mp번의 내적, 매번 n번의 곱셈
cf-2) 열×행: n번의 외적, 매번 mp번의 곱셈
1.2.2 열과 행의 곱셈에 대한 이해
Data Science에서 외적을 이용한 행렬곱셈이 필수인 이유는?
- 간단히 말해, 특정 행렬에서 "어떤 중요부분을 찾으려"하기 위해.
행렬 A, B에 대해
- B의 행의 일차결합을 얻고 싶을 때: AB
- B의 열의 일차결합을 얻고 싶을 때: BA
즉, AB의 열은 A의 열의 일차결합이고 행은 B의 행의 일차결합이다.
- 따라서 AB의 열공간은 A의 열공간에 포함된다.
응용선형대수학에서 가장 중요한 주제는 A를 CR로 분해하는 것이다.
그리고 A = CR에서 cₖrₖ를 살펴보고자 할 때, 중요.
5개의 중요한 행렬 분해
1. A = LU
- L은 하삼각행렬, U는 상삼각행렬이다.
2. A = QR
- 그람-슈미트(Gram-Schmidt)를 통해 열 a1, ..., an을 직교화(orthogonalizing)하여 얻는다.
- R은 상삼각 행렬이며 이때, Q에 정규직교인 열이 있다.(QTQ = I)
3. S = QΛQT
- 대칭행렬(Symmetric matrix) S = ST의 고윳값 λ1, ... , λn에서 얻는다.
- 이때, Λ는대각성분의 고윳값(eigen value)
- Q의 열은 정규직교인 고유벡터(eigen vector) , QT = Q⁻¹
4. A = XΛX⁻¹
- 대각화(diagonalization)는 행렬에 일차독립인 고유벡터가 n개일 때, 가능
- Λ의 대각성분은 고윳값이며, X의 열은 A의 고유벡터이다.
5. A = U∑VT
- 임의의 A행렬의 특잇값분해(Singular Vector Decomposition; SVD)이다.
- ∑의 성분에는 특잇값 σ1, ... , σr이 있다.
- U와 V에는 정규직교인 특이벡터(singular vector)가 존재.
Ex. S = QΛQT
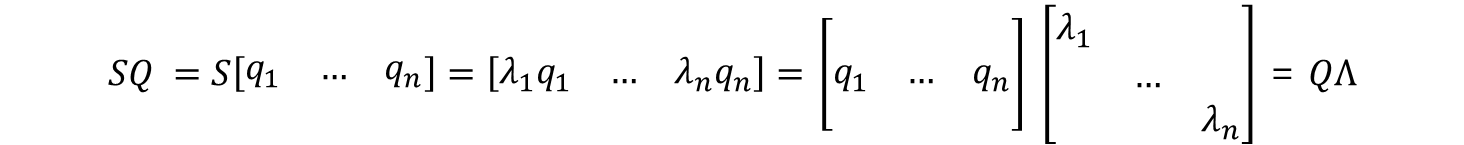
Q⁻¹ = QT이므로 SQ = QΛ의 양변에 QT를 곱하면 S = QΛQT = 대칭행렬을 얻는다.
각 고윳값 λₖ와 고유벡터 qₖ는 rank=1인 행렬인 λₖ qₖ qₖT를 만든다.
- rank = 1인 행렬 : S = (QΛ)QT = (λ₁ q₁) q₁T + ... + (λn qn) qnT
- 모두 대칭 : qiqiT의 전치행렬은 qiqiT이다.
스펙트럼 정리 (spectrum theorem) S = (QΛ)QT
모든 대칭행렬 S는 n개의 실수인 고윳값과 n개의 정규직교인 고유벡터를 갖는다.
S = ST일 때, S의 고윳값은 실수이다.
cf. 증명에서 조심해야할 부분: 고윳값 λi가 반복될 때
- 다항식이 중근을 갖거나 (λ - λj)M 형태로 인수분해된다.
- 이 경우, M개의 일차독립인 고유벡터를 찾아야 한다.
- 이때 행렬 S - λjI의 rank = n - M이다. (단, S = ST일 때 가능)
cf-2. 마찬가지로 A = U∑VT또한 대각행렬 ∑에서 특잇값 σ가 M번 반복될 때, 주의
- 즉, Av = σu를 만족하는 Singular Vector v와 u쌍이 M개 존재해야함을 의미.
'Gain Study > Linear Algebra & Learning from Data' 카테고리의 다른 글
| 1.4 소거법과 A = LU분해, Cholesky분해 (0) | 2023.06.29 |
|---|---|
| 1.3 4가지 fundmental subspaces (0) | 2023.06.29 |
| 1.1 Ax = b의 space와 independent, rank (0) | 2023.06.27 |
| Part 0. Previews & Index (0) | 2023.06.27 |

