

※ 이번 문제에서 알게된 점
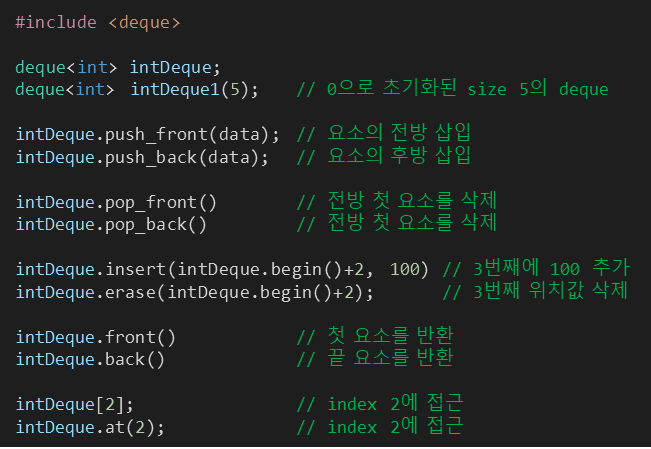
§ insert() 함수
dq.insert함수는 insert(pos, val);로 값이 들어가야 해서 dq.insert(dq.end()+i, dq.begin()+i);처럼 사용하지 말아야 한다.
위와 같은 의미로 다시 코드를 짜고 싶다면 다음과 같이 dq.insert(dq.end()+i, dq[i]); 와 같이 사용해야 한다.
dq.insert(dq.end()+i+1, dq[i]); // 정상적인 작동
dq.insert(dq.end()+i+1, dq.begin(i)); // dq.begin(i) 부분에 오류발생
dq.insert(dq.end()+i+1, dq.begin()+i); // dq.insert() 부분에 오류발생
§ front 와 begin 의 차이
가장 고생했던 부분이 있는데 다음과 같다.
<정답코드>
for (int i = 0; i < k-1; i++) {
dq.push_back(dq.front());
dq.pop_front();
}
cout << dq.front() << ", ";
dq.erase(dq.begin());
// 7 3
// <3, 6, 2, 7, 5, 1, 4>
<오답코드>
for (int i = 0; i < k; i++) {
dq.insert(dq.end()+i+1, dq[i]);
dq.erase(dq.begin()+i);
}
dq.pop_back();
// 7 3
// <2, 4, 7, 7, 7, 7, 7>
front()는 첫 "요소"를 반환하는 것이다.
begin()은 그 요소의 참조 즉, "주소값"을 반환한다.
즉, begin은 컬렉션을 통해 반복하는 데 사용할 수 있는 해당 요소의 iterators를 반환하지만
front는 컬렉션의 첫 번째 요소에 대한 참조만 반환 (포인터 개념)합니다.
따라서 push_back(값); 메소드를 활용하기 위해서는 front를 사용하는 것이 좋다.
dq.push_back(dq.front());
§ my solution
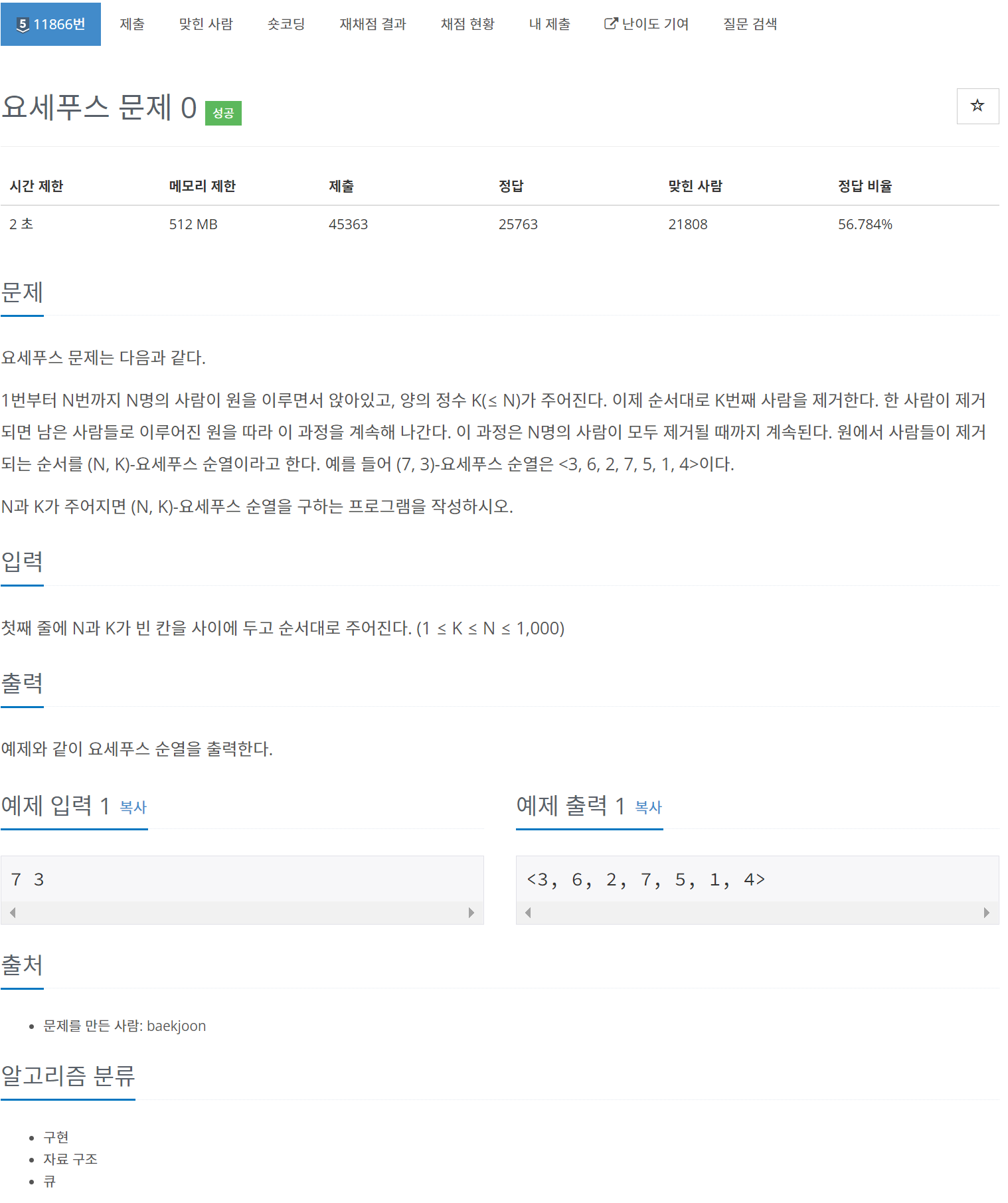
추출,삽입이 빠른 덱으로 k - 1번씩 밀고, 맨 앞에있는 값을 제거하는 알고리즘을, 모든 값이 없어질 때 까지 반복
#include <iostream>
#include <deque>
using namespace std;
deque<int> dq;
int main(){
int n, k; cin >> n >> k;
cout << '<';
for (int i = 0; i < n; i++) {
dq.push_back(i+1);
}
while (dq.size() > 1) {
for (int i = 0; i < k-1; i++) {
dq.push_back(dq.front());
dq.pop_front();
}
cout << dq.front() << ", ";
dq.erase(dq.begin());
}
cout << dq[0];
cout << '>';
}
§ 시행착오
#include <iostream>
#include <deque>
using namespace std;
deque<int> dq;
int main(){
int n, k; cin >> n >> k;
cout << '<';
for (int i = 0; i < n; i++) {
dq.push_back(i+1);
}
while (dq.size() > 1) {
if (dq.size() > 2) {
cout << dq[k-1] << ", ";
for (int i = 0; i < k; i++) {
dq.insert(dq.end()+i+1, dq[i]);
dq.erase(dq.begin()+i);
}
dq.pop_back();
}
else if(dq.size() <= 2){
cout << dq[0] << ", "<< dq[1];
break;
}
}
cout << dq[0];
cout << '>';
}왜 이따구로 풀었을까?
- 일단 먼저 다음과 같이 접근하였다.
1 2 3 4
7 6 5
front back <-- 삽입
1 2 3 4 5 6 7
(1 2 3) 4 5 6 7 [1 2 3]
4 5 6 7 1 2
(4 5 6) 7 1 2 [4 5 6]
7 1 2 4 5
4 5 7 1
1 4 5
4 5 1
>> 그대로 출력 5 1 4왜 안될까? => k값이 3이라 저렇게 출력되는 것처럼 보일 뿐, 다음과 같은 테스트 케이스에서는 오답으로 나온다.
10 1
<1, 2, 3, 4, 5, 6, 7, 8, 9, 10>
5 5
<5, 1, 3, 4, 2>
10 4
<4, 8, 2, 7, 3, 10, 9, 1, 6, 5>따라서 예제의 특수성에 빠지지 않도록 조심할 것!
'Algorithms > Coding Test' 카테고리의 다른 글
| [Baekjoon/백준] 10867번: 중복 빼고 정렬하기(C/C++) (0) | 2022.11.03 |
|---|---|
| [Baekjoon/백준] 11728번: 배열 합치기_merge(C/C++) / (알게된 점 多) (0) | 2022.11.03 |
| [Baekjoon/백준] 2161번: 카드1_deque(C/C++) / (알게된 점X) (0) | 2022.11.02 |
| [Baekjoon/백준] 2164번: 카드2_deque(C/C++) / (알게된 점X) (0) | 2022.11.02 |
| [Baekjoon/백준] 10828번: 스택_stack(C/C++) (0) | 2022.11.01 |